Measure twice, cut once
I reflect often on a joke my trigonometry teacher told our class back in high school:
“How do you kill a blue elephant?”
“I don’t know, how?”
“A blue elephant gun. How do you kill a red elephant?”
“I don’t know, how?”
“A red elephant gun. How do you kill a white elephant?”
“A white elephant gun?”
“No, silly, there’s no such thing as a white elephant gun! You hold the elephant’s trunk until it turns blue, then use a blue elephant gun.”
She told us the joke because we were starting a unit on coordinate transformation. Basically, some curves are really hard to write equations for in their given coordinates, but are easy to write easy to write equations for in transformed coordinates.
Further down the mathematical education line, I learned about a fancier application of the same idea. A Fourier transform takes an equation in one “domain” and turns it into an equation in another “domain.” The most common transformation is between time and frequency. Here is an example from the Wikipedia page showing how a square wave in the time domain - a pretty complicated function - breaks down into a few discrete values in the frequency domain. Engineers and physicists use the Fourier transform regularly to understand the individual factors driving complex behavior.
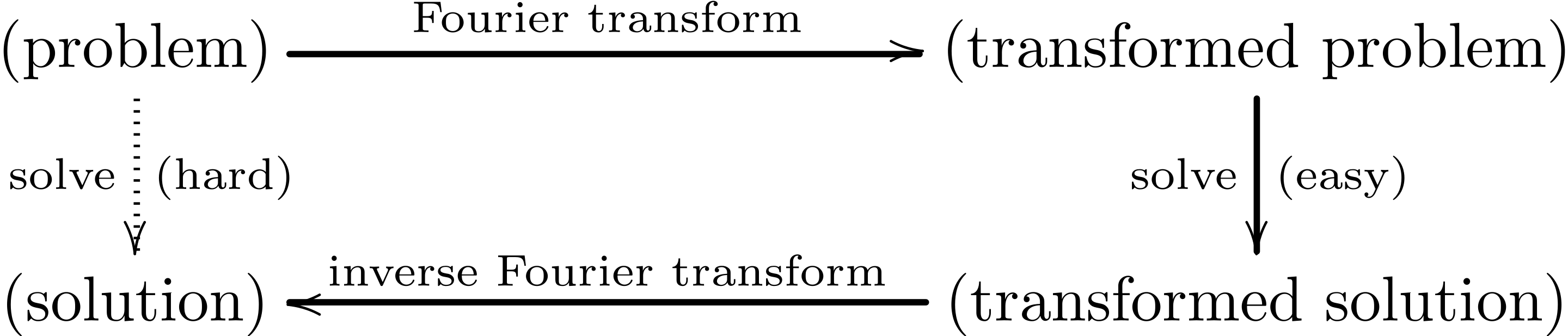
In each case, the lesson is the same: the best way to solve a hard problem is to turn it into an easy problem. The trick is studying the problem until you know how to transform it. In the words of pioneering computer scientist Alan Kay, “Perspective is worth 80 IQ points.”
As a result, I spend most of my time on a project or product researching, thinking about, and analyzing the problem. What does it include? What is extraneous? What are the key metrics? What have we tried to solve it before? What have other people tried? What levers can we pull? What is out of our control? Ask yourself enough such questions and eventually you will reconceptualize the problem - you will transform it from a white elephant into a blue elephant, from the time domain into the frequency domain. Once you transform your problem, the solution will become obvious.